■ エノン写像
    \[ f_{a,b}:(x_1,x_2)\mapsto(1-ax_1^2+x_2,bx_1),\quad (x_1,x_2)\in\mathbb{R}^2,\quad a,b\in\mathbb{R} \]


    天文学者のエノン (Michel Hénon) は1976年に発表された論文で， $(a,b)=(1.4,0.3)$のとき
    この単純な2次元写像が複雑な挙動を示すことを 数値実験 (数値シミュレーション) により示した．

    $b=0.3$ に固定して， ロジスティック写像の場合と同様に， 写像 $f_{a,b}$ を繰り返し作用させるとき，
    点 $(x_1,x_2)$ がどのように変化していくのか その様子を見てみよう．

    まず，初期点を $(x_1,x_2)=(0.5,-1)$ とする．

    • "hm1.py"を使用 (クリックすると，Pythonのプログラムをダウンロード可能)

      $a=0.2$ に対する軌道



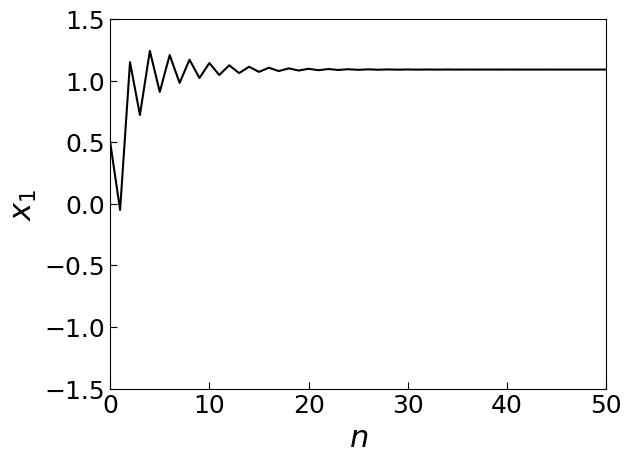
      繰り返し数 $n\to\infty$ のとき軌道は不動点に収束する．

    • "hm2.py"を使用

      $a=0.5$ に対する軌道



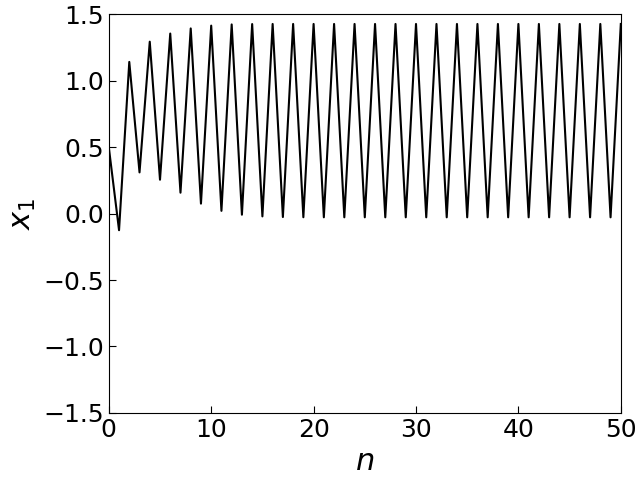
      繰り返し数 $n\to\infty$ のとき軌道は周期2の安定周期軌道に収束する．
      $a=0.3$ と $0.5$ の間で周期倍加分岐が起きている．

    • "hm3.py"を使用

      $a=1$ に対する軌道



      繰り返し数 $n\to\infty$ のとき $x_n$ は周期4の安定周期軌道に収束する．
      $a=0.5$ と $1$ の間で再び周期倍加分岐が起きている．

      引き続き，$a$ の値を増加させていくと，ロジスティック写像の場合と同様に，
      次々と周期倍加分岐が起こり，周期 $2^k$ ($k$ は4以上の自然数) の周期軌道が発生する．
      （プログラムhm3.pyの"a = 1"の行を変更して実行し，確認してみよう．）

    • "hm4.py"を使用

      $a=1.4$ に対する軌道



      いつまでたっても軌道にこれまでのような規則性はみらず，カオスが起きている．

    上では変数 $x_1$ の変化のみに着目していたが，エノン写像は2次元写像である．
    変数 $x_2$ も含めて，$(x_1,x_2)$ 平面上で上の軌道を見てみよう．

    • "hm5.py"を使用

      $a=0.2$ に対する軌道



      白丸は初期点と $n=50$ のときの点である． $n\to\infty$ のとき軌道は不動点に収束している．

    • "hm6.py"を使用

      $a=0.5$ に対する軌道



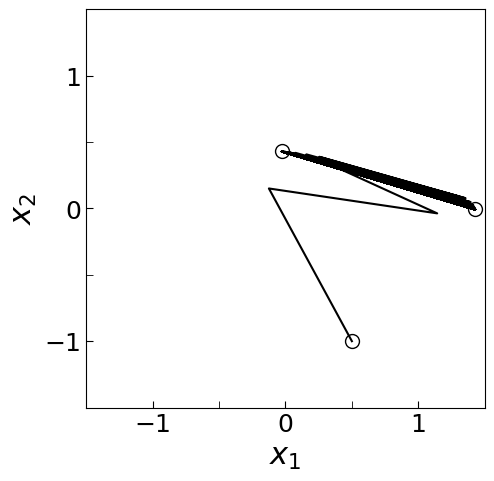
      白丸は初期点と $n=49,50$ のときの点である． $n\to\infty$ のとき軌道は周期2の安定周期軌道に収束している．
      $a=0.3$ と $0.5$ の間で周期倍加分岐が起きている．

    • "hm7.py"を使用

      $a=1$ に対する軌道



      白丸○は初期点と $n=47$ から $50$ までのの点である．
      $n\to\infty$ のとき $x_n$ は周期4の安定周期軌道に収束している．
      $a=0.5$ と $1$ の間で周期倍加分岐が起きている．

      上で述べたように，引き続き，$a$ の値を増加させていくと，次々と周期倍加分岐が起こり，
      周期 $2^k$ ($k$ は4以上の自然数) の周期軌道が発生する．
      （プログラムhm7.pyの"a = 1"の行を変更して実行し，確認してみよう．）

    • "hm8.py"を使用

      $a=1.4$ に対する軌道 ()



      $n>1000$ のときの点をプロットし，計算された点は折線でつないでいない． 軌道はとても複雑である．
      $n\to\infty$ としたときの収束先の軌道を アトラクタといい，
      この例のように，不動点，周期軌道，不変トーラス (準周期軌道) と異なるアトラクタを ストレンジ・アトラクタという．

    上の図で点 $(0.065,1)$ と $(0.115,1.15)$ を2頂点とする領域を20倍に拡大してみよう．

    • "hm9.py"を使用

      $a=1.4$ に対する軌道



      上の図で1本の曲線に見えていたものが，何本かの曲線からなっていたことがわかる．

    さらに，点 $(0.065,1)$ と $(0.115,1.15)$ を2頂点とする領域を20倍に拡大する．

    • "hm10.py"を使用

      $a=1.4$ に対する軌道



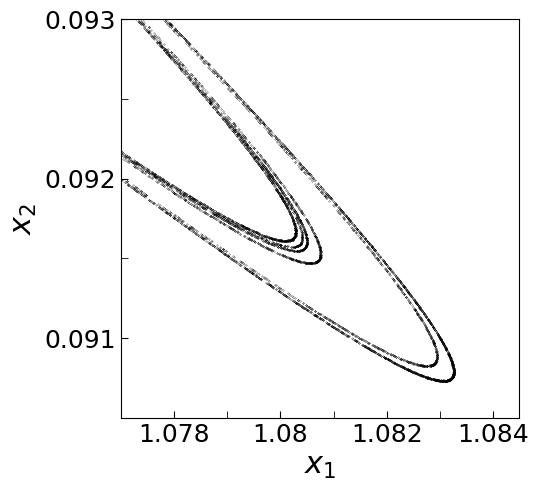
      再び，上の図で1本の曲線に見えていたものが，何本かの曲線からなっていたことがわかる．
      このように，拡大していくとき，同じようなものが繰り返し現れる幾何学的な構造を フラクタルという．
      この例のように，ストレンジ・アトラクタは普通フラクタル構造を有している．

    ロジスティック写像のときと同様に，$n$の値を大きくしていったときの軌道は制御パラメータ$a$の値に
    非常に依存したものとなっている． その変化の様子をもう少し詳しく調べてみよう．

    • "hmb1.py"を使用

      横軸を $b$，縦軸を $x_1$ として， 繰り返し数 $n$ が201から400までの点をプロット



      ロジスティック写像の場合と同様に，安定な不動点からカオスに至るまで，
      たくさんの（実は無限個の）周期倍加分岐が起きていることがわかる．

    上の図でカオスが起きてそうなパラメータ $a$ の範囲 $[1.29,1.31]$ を拡大してみよう．

    • "hmb2.py"を使用

      区間 $[1.29,1.31]$ の $a$ に対して， 繰り返し数 $n$ が$201$から$400$までの点をプロット



      ロジスティック写像のときと同様に，カオスが起きているような $a$ の値の範囲でも，
      周期軌道の存在する範囲があり，そのような状態から先の図で見たのと同じようなプロセスを経て
      再びカオスに至っている．

      力学系の数値シミュレーション・トップページに戻る



    無断転載禁止

    Latest Updating is on April 9, 2024.