■ ロジスティック写像
    \[ f_a:x\mapsto ax(1-x),\quad x\in[0,1]\quad \text{($a\in[0,4]$ は定数)} \]


    関数 $f_a$ のグラフは下図のように，頂点が $(1/2,a/4)$ の上に凸の放物線である．



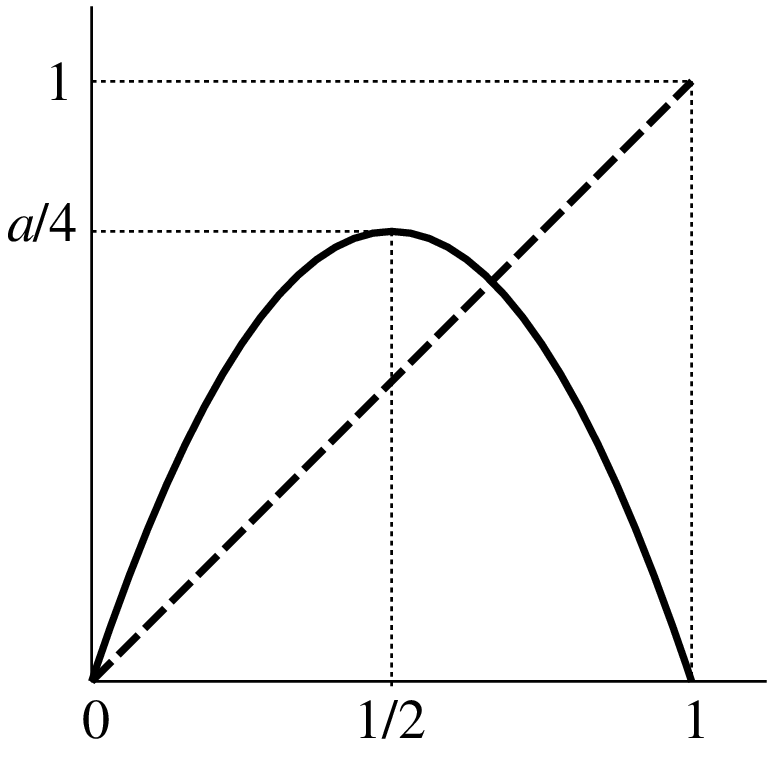
    生態学では，多くの昆虫のように世代が重ならないような生物 の個体数を記述する単純なモデルとして用いられている．

    初期値 $x_0\in[0,1]$ に対して写像 $f_a$ を繰り返し作用させるとき， \[ x_n=f_a^{n}(x)=\underbrace{f_a\circ f_a\circ\cdots\circ f_a}_{n}(x) \] の値がどのように変化していくのか，以下ではその様子を見てみよう．

    まず，初期点を $x_0=0.5$ に固定する．

    • "lm1.py"を使用 (クリックすると，Pythonのプログラムをダウンロード可能)

      $a=0.9$ に対する軌道



      繰り返し数 $n\to\infty$ のとき $x_n$ は $0$ に漸近する．
      一般に，ある写像を作用しても変化しない点をその写像の不動点という．
      また，その近傍の軌道が$n\to\infty$ のとき不動点に収束している場合，その不動点は安定であるという．
      $a=0.9$ のとき，$x=0$はロジスティック写像 $f_a$ の安定な不動点である．

    • "lm2.py"を使用

      $a=2.8$ に対する軌道



      繰り返し数 $n\to\infty$ のとき $x_n$ は $0$ と異なる値に漸近し， 上の場合と異なる安定な不動点に収束している．
      $a$のようなパラメータを変化させたとき， 挙動が突然定性的に変化する現象を分岐という．
      上の結果と比較すると，$a=0.9$ と $2.8$ の間で分岐が起きていることになる．
      また，分岐を観測するために変化させられるパラメータ (この場合は$a$) を 制御パラメータと呼ぶ．

    • "lm3.py"を使用

      $a=3.05$ に対する軌道



      繰り返し数 $n\to\infty$ のとき $x_n$ は2つの値の間を振動し，周期2の周期軌道が発生する．
      その近傍の軌道は $n\to\infty$ のときそれに収束しているので，この周期軌道は安定である．
      不動点を周期1の周期軌道とみなすと，その2倍の周期をもつ周期軌道が発生していることになる．
      また，$a=2.8$の場合の結果と比較すると，$a=2.8$ と $3.05$ の間で分岐が起きていることがわかる．
      このような分岐は周期倍加分岐と呼ばれる．

    • "lm4.py"を使用

      $a=3.5$ に対する軌道



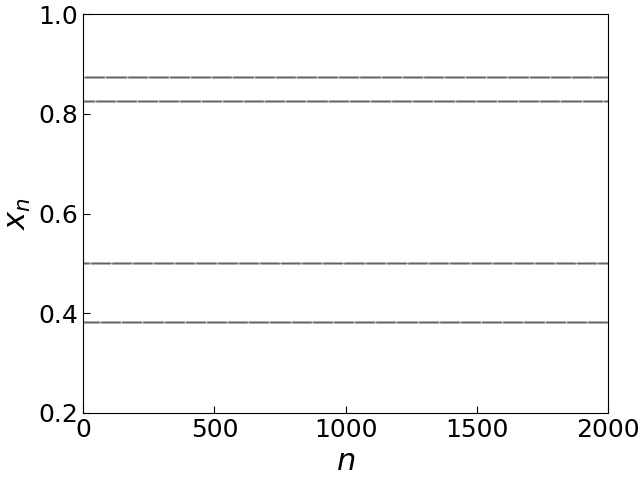
      繰り返し数 $n\to\infty$ のとき $x_n$ は4つの値の間を振動し，周期4の安定な周期軌道が発生する．
      ここで，計算された点$(n,x_n)$は直線で結ばれていない．
      上の結果と比較すると，$a=3.05$ と $3.5$ の間で周期倍加分岐が起きていることがわかる．

    • "lm5.py"を使用

      $a=3.56$ に対する軌道



      繰り返し数 $n\to\infty$ のとき $x_n$ は8つの値の間を振動し，周期8の安定な周期軌道が発生する．
      上の結果と比較すると，$a=3.5$ と $3.56$ の間で周期倍加分岐が起きていることがわかる．

      引き続き，$a$ の値を増加させていくと，次々と周期倍加分岐が起こり，
      周期 $2^k$ ($k$ は4以上の自然数) の周期軌道が発生する．
      （プログラムlm5.pyの"a = 3.5"の行を変更して実行し，確認してみよう．）

    • "lm6.py"を使用

      $a=3.6$ に対する軌道



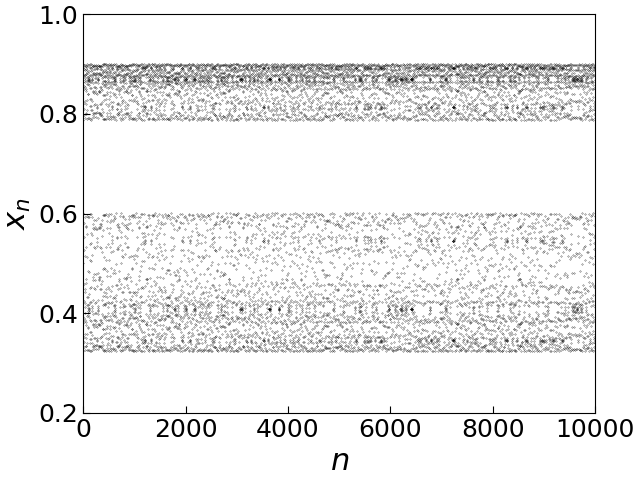
      いつまでたっても軌道にこれまでのような規則性はみられない．
      このような現象をカオスという．

    カオスにはその軌道が初期値に敏感に依存するという初期値鋭敏性という性質がある．
    これは，比喩的に
     「北京でバタフライがはばたくとニューヨークの天気が変わる」
    と言い表されることから，バタフライ効果とも呼ばれる．
    次に，この現象を見てみよう．

    • "lm7.py"を使用

      $a=3.6$，$x_0=0.5$ (黒) と$0.501$ (赤) に対する軌道



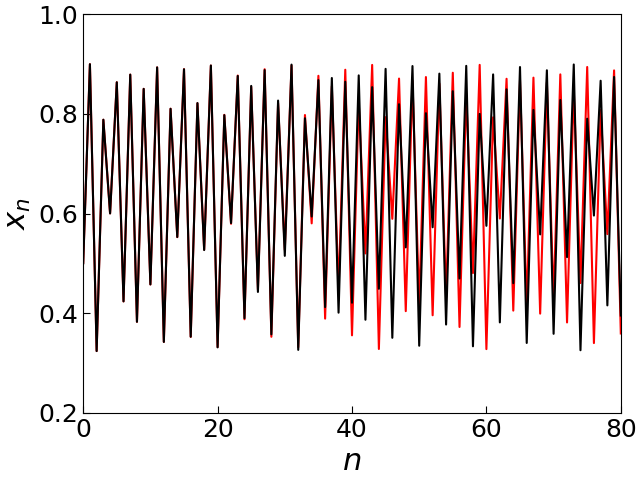
      $n=40$ のあたりまでは2つの軌道はほぼ一致しているが，それを過ぎると大きく異なっている．
      このように，カオスが起こっているとき， （例えば，北京で蝶々がはばたいくような）少しの変動でも，
      その影響は時間の経過とともに非常に大きなものとなり， 最終的にはまったく異なった結果となってしまう
      （ニューヨークの天気が変わる）ということが起こる．

    これまで見てきたように，$n$の値を大きくしていったときの軌道は 制御パラメータ$a$の値に非常に依存したものとなる．
    その変化の様子をもう少し詳しく調べてみよう．

    • "lmb1.py"を使用

      横軸を $a$，縦軸を $x_n$ として， 繰り返し数 $n$ が201から400までの点をプロット



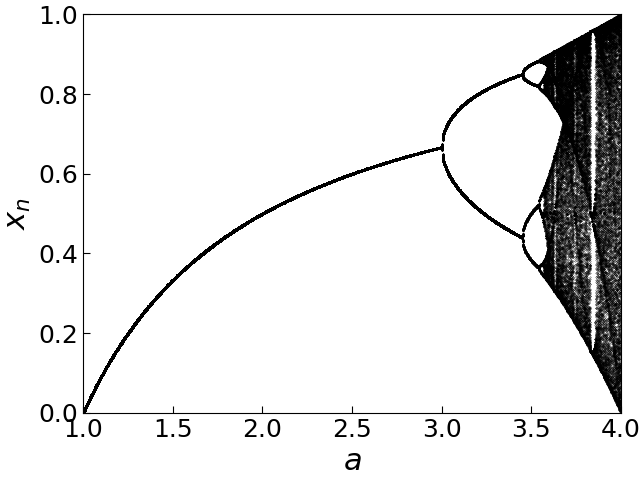
      $a$ の値を固定して見たとき，
      ひとつだけプロットされている場合は $n$ を大きくしていくと， $x_n$ はある不動点に近づいていることになる．
      また，2つプロットがある場合は周期2の周期軌道， 4つプロットがある場合は周期4の周期軌道に収束していることになる．
      さらに，たくさんプロットされている場合では， $x_n$がいつまでたっても規則的にならず，カオスが起きていることになる．
      安定な不動点からカオスに至るまで，たくさんの（実は無限個の）周期倍加分岐が起きていることがわかる．
      このような図を分岐ダイアグラムという．

    上の図でカオスが起きてそうなパラメータ $a$ の範囲 $[3.82,3.86]$ を拡大してみよう．

    • "lmb2.py"を使用

      区間 $[3.82,3.86]$ の $a$ に対して， 繰り返し数 $n$ が$201$から$400$までの点をプロット



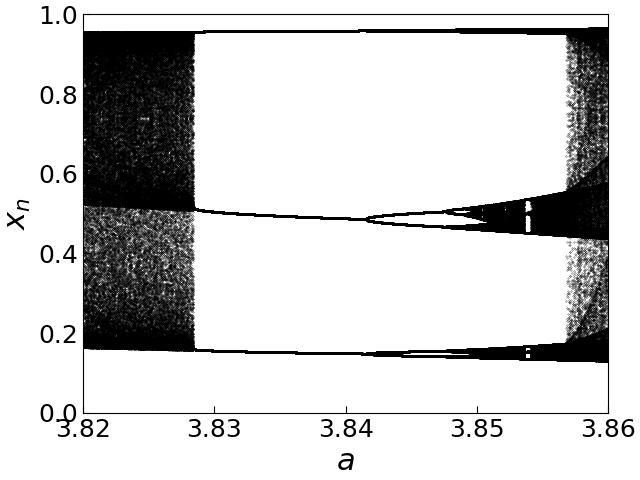
      カオスが起きているような $a$ の値の範囲でも，周期軌道の存在する範囲があり，
      そのような状態から先の図で見たのと同じようなプロセスを経て 再びカオスに至っている．

      力学系の数値シミュレーション・トップページに戻る

    無断転載禁止

    Latest Updating is on December 20, 2023.