エノン・ハイレス系2

$c=1$，$d=-1$ とする．エノンとハイレスの行った計算に従い，まず $H=0.08333$ の場合に対してポアンカレ写像 $P$ の軌道を計算する．

"hh8.py"を使用

$H=0.08333$ の場合のポアンカレ写像 $P$ の軌道

$c,d=1$ の場合と同様に，軌道の多くは準周期的である．
エノンとハイレスは，このように，ハミルトン関数の値が小さなレベル集合では，可積分系と同様な挙動を示し，これは
ハミルトン関数とは他の第1積分の存在を示唆していると述べている (現在では，この予想は間違いであることが明らかにされている)．
また，彼らは特に指摘していなかったが (おそらく，計算精度が十分でなかったこともあり，気が付かなかったのであろう)，
このようなハミルトン関数の値が小さなレベル集合においても準周期的 (あるいは周期的) でない軌道は実は複雑な挙動を示している．

上の図の点 $(x_1,x_3)=(-0.12,0)$ の近くを拡大した図を描いてみよう．

"hh9.py"を使用

$H=0.08333$ の場合のポアンカレ写像 $P$ の軌道 (拡大)

このように，軌道は準周期的ではなく，カオス現象が起きていることが確認できる．

続いて，エノンとハイレスと同様に $H=0.125$ の場合を考える．

"hh10.py"を使用

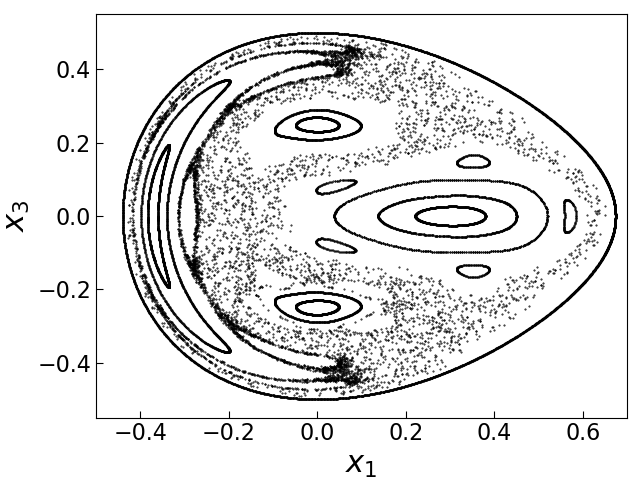
$H=0.125$ の場合のポアンカレ写像 $P$ の軌道

レベル集合のより広い範囲に渡ってカオス軌道が広がってで覆い尽くされてしまっていることがわかる．

さらに，エノンとハイレスと同様に $H=0.16667$ の場合を考える．

"hh11.py"を使用

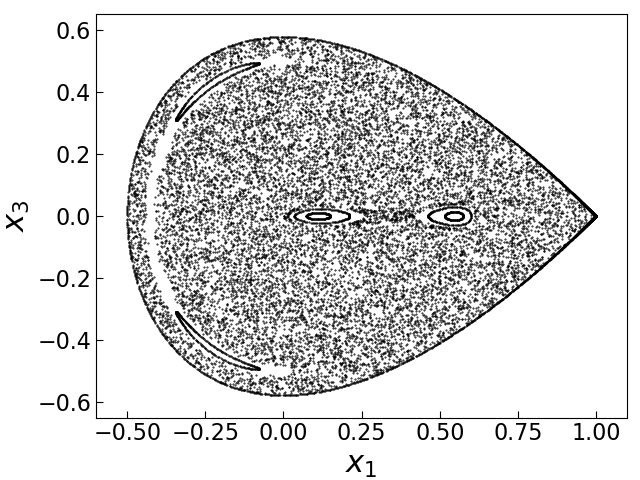
$H=0.16667$ の場合のポアンカレ写像 $P$ の軌道

レベル集合はほとんどカオス軌道で覆い尽くされている．

エノン・ハイレス系で見られるこのような挙動は，可積分でない多くのハミルトン系で起こることが現在では知られている．

力学系の数値シミュレーション・トップページ