準定常状態
分布関数による記述
1体分布関数
N個の粒子からなる系をそのまま調べようとすると、
N個の位置ベクトル(q1,...,qN)とN個の運動量ベクトル(p1,...,pN)をそのまま扱わないといけません。
これは大変です。
(q1,p1), (q2,p2), ..., (qN,pN) という N個の組が作る分布の時間発展を調べよう、
という方法があります。
この分布関数 f(q,p,t) を1体分布関数と言います。
q や p の次元は、q1 や p1 と同じです。
方程式
f(q,p,t) が従う方程式は、だいたい次のような形です。
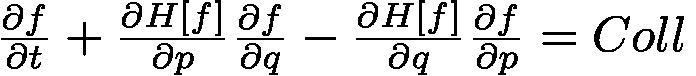
- H[f]は、fから定まる1体ハミルトン汎関数です。
- Coll は二体衝突を表すような項で、衝突項と呼ばれます。
ここまでは、厳密な変形で行けます。
ただし、Coll を得るには1体分布関数だけではダメで、
- 1体分布関数の時間発展を得るには2体分布関数と呼ばれるものが必要で、
- 2体分布関数の時間発展を得るには3体分布関数と呼ばれるものが必要で、
- 3体分布関数の時間発展を得るには4体分布関数と呼ばれるものが必要で、
と結局はN体まで戻らないといけなくなります。
それでは何も嬉しくないので、上の鎖を何とか断ち切りたくなります。
Good news!
長距離相互作用系においては、
粒子数無限の極限で Coll=0としてよいということが、
数学的に証明されています。
ざっくり言うと、粒子数 N に対して、Coll=O(1/N) くらいで小さくなります。
Vlasov方程式
Coll=0 とした
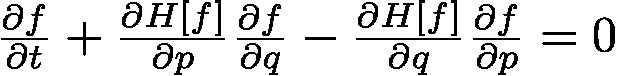をVlasov方程式と言います。
Vlasov方程式の定常解と安定性
定常解は無限にある
Vlasov方程式には、無限の定常解が存在します。
左辺の第2,3項の和がゼロということです。
例えば、f(q,p) が q に依存しないとき、往々にして定常解となります。
安定性が問題
定常状態に対しては、その安定性を議論することができます。
安定であれば、多少の摂動があったとしても、
その状態の付近からずっと動かないことを意味します。
それがたとえ、非熱平衡状態であったとしてもです。
だんだん、準定常状態に近づいてきました。
準定常状態
安定定常状態 : 粒子数無限の場合
Vlasov方程式は粒子数無限の極限で成り立つ式でした。
安定定常状態があれば、非熱平衡状態であったとしても動かない、
つまり熱平衡状態に緩和しません。
安定定常状態 : 粒子数有限の場合
ところが、粒子数が有限Nであれば、Coll=0 とはできません。
Coll=O(1/N) 程度残ります。
この小さい衝突項が系を熱平衡状態にゆっくりと運びます。
準定常状態の解釈
以上から、準定常状態とは、
- 粒子数無限の極限でVlasov方程式の安定定常解に対応する状態
- 粒子数有限では、衝突項のせいで熱平衡状態へとゆっくり緩和する
- 緩和はゆっくりなので、長時間同じ状態に留まっているように見える
と解釈できます。
本当に定常だと動きませんが、ゆっくりでも動くので「準」が付きます。
準定常状態は熱平衡状態も含むより広い概念
熱平衡状態も Vlasov 方程式の安定定常状態になっています。
つまり準定常状態は熱平衡状態も含むより広い概念です。
広い概念ということは、解析がより難しくなりますが、
より多様な現象が観測できることも意味します。
実際、
- 熱平衡状態では観測されない相転移が観測されたり、
- 従来の統計力学が予測する値とはことなる臨界指数が観測されたり
という新奇な現象が観測されています。
Last modified: Mon Jun 20 14:44:58 JST 2016